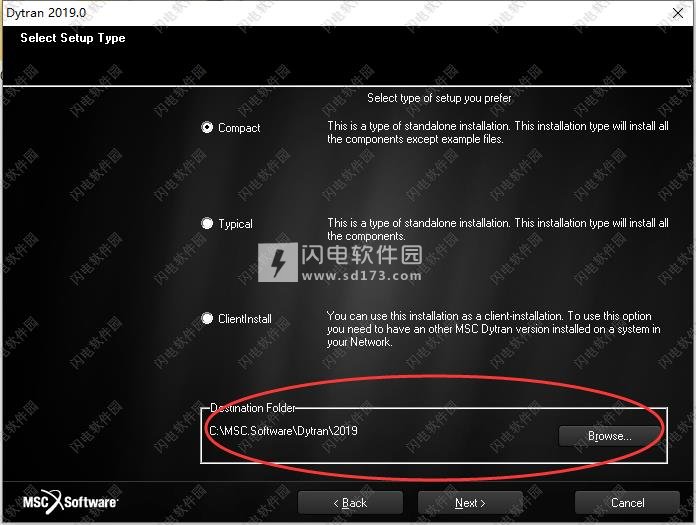
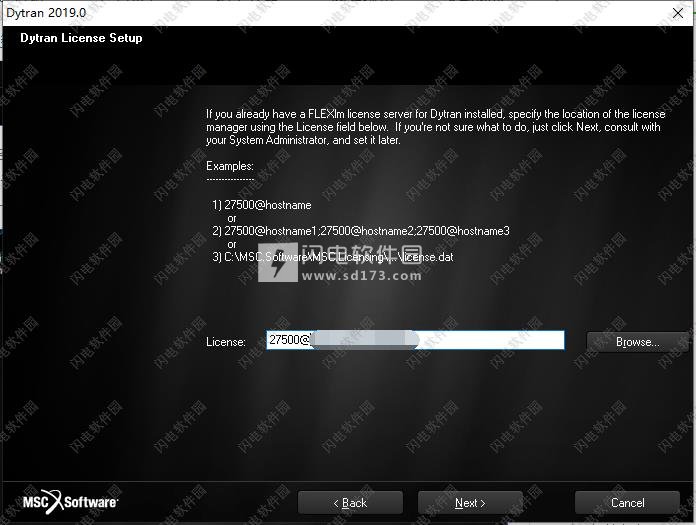
。Dytran格式的ATB输出
软件特色
1、针对不同应用的准确,稳健的分析
通过与物理实验的相关性证明了Dytran的准确性。 Dytran帮助工程师预测原型如何响应各种现实世界的动态事件,并检查产品失效的潜在原因。一些例子包括:
·航空航天应用:飞机开沟,油箱晃动和破裂,鸟击模拟,发动机叶片遏制,飞机耐撞性,座椅设计和安全,飞机和货物围护硬化。
·汽车应用:安全气囊设计和乘员安全(不在位置研究),假人造型和座椅设计,车辆碰撞和碰撞测试,轮胎打滑,油箱晃动和破裂。
·军事和国防应用:异型充电模拟和武器设计,射弹穿透和目标穿孔,水动力冲击(HRAM),船舶碰撞,水下冲击爆炸(UNDEX),抗爆炸和生存能力。
·其他工业应用:瓶子和容器设计,送纸,跌落测试,运动器材影响分析,包装设计。
2、模拟技术的独特组合
Dytran在单个仿真包中提供结构,材料流和耦合FSI分析。显式非线性求解器技术用于分析极端,短时,瞬态事件,这些事件需要更精细的时间步骤来确保解决方案的准确性和稳定性。
这允许您模拟涉及(i)高度材料非线性的FEA问题,
(i)大的几何非线性,和(fi)极端边界非线性。
Dytran利用拉格朗日求解器以高精度监测结构中的位移和应力。复杂的材料流动采用先进的多材料欧拉求解器技术建模,对模拟材料的变形量没有限制。拉格朗日之间的相互作用Eulerian有限元网格是通过Dytran独特的直接耦合特征实现的,可以在一个连续模拟中对流体和高度可变形材料的结构组件进行综合分析,从而快速,轻松地为您提供预测结果。
Dytran创建的能够在耦合曲面移动和变形时模拟自适应多个欧拉域的交互,使您能够分析复杂的FSI场景,这些场景通常太难或无法用其他软件工具模拟,例如:
·影响多层结构的多个物体(例如,确定在飞行中多次鸟撞击飞机结构的影响)。
软件功能
1、先进的显式非线性求解器技术,用于模拟和分析极端,短时动态事件,例如各种工业和商业应用中的材料的碰撞,挤压,冲击,跌落,冲击,摇晃,爆炸,穿透和晃动。
2、使用拉格朗日有限元法进行结构分析的鲁棒有效的三维接触和耦合算法以及用于流体和多材料流动分析的欧拉有限体积法。
3、完整的有限元模型库,包括梁,壳,固体,弹簧和具有大排量配方的阻尼器。
4、适用于金属,复合材料,土壤,泡沫橡胶,液体和气体的全系列非线性材料模型。
5、分布式内存并行(DMP)支持欧拉解算器和耦合表面计算
6、通过Dytran的简化建模流程和最先进的流体 - 结构交互(FSI)仿真功能,最大限度地降低物理原型设计的成本并消除冗余测试周期。
7、快速获得对其他仿真工具无法轻易解决的现实问题的非线性动态行为的详细了解。
8、模拟复杂场景并执行“假设”
在单个分析包和模拟环境中,在设计周期的早期进行分析。
9、应用Dytran的结果来提高产品质量,并将失败的可能性和重新设计成本降至最低。
使用帮助
1、拉格朗日求解器
网格点是模型几何的基本定义。网格点的空间坐标在GRID批量数据条目上定义。每个网格点最多可以有六个位移分量或自由度,具体取决于网格点所连接的元素。这些自由度是基本坐标系中的三个平移分量和三个旋转分量。可以使用GRIDentry上的字段或使用其中一个SPCn条目将永久单点约束应用于拉格朗日网格点。可以在三个平移分量(1,2,3)和三个旋转分量(4,5,6)的任何组合中约束网格点。
实体,板和梁元件可以通过连接到公共网格点而连接在一起。该连接用作铰链,其中三个DOF元件(固体)连接到六个DOF元件
(板/束)。如果需要连接旋转自由度,则可以使用KJOlN条目。
2、欧拉解算器
网格点的定义对于欧拉和拉格朗日求解器都是通用的。网格点是模型几何的基本定义。网格点的空间坐标在GRID批量数据条目上定义。
虽然拉格朗日网格点最多可以有六个位移分量,但用于定义欧拉元素的网格点具有零或三个自由度。这些网格点是用于定义欧拉网格的空间位置的几何设备。
拉格朗日和欧拉元素不能有共同的网格点。如果要连接拉格朗日元素和欧拉元素,则必须为两个元素类型创建单独的网格点,然后使用ALE和SURFACE批量数据条目。
3、网格点排序
 MSC DYTRAN 2024.2 x64 破解版 含教程
MSC DYTRAN 2024.2 x64 破解版 含教程
 MSC DYTRAN 2024.2 x64 破解版 含教程
MSC DYTRAN 2024.2 x64 破解版 含教程