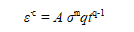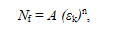Marc 2020破解版是功能强大的非线性仿真解决方案,具有强大的功能,可用于准确快速的模拟产品的各种行为,包括各种不同的情况,如静态、动态或者是多物理场加载的情况,模拟结果比较的准确,快速获得结果,并且能够在非线性材料建模以及瞬态环境条件方面具有
Marc 2020破解版是功能强大的非线性仿真解决方案,具有强大的功能,可用于准确快速的模拟产品的各种行为,包括各种不同的情况,如静态、动态或者是多物理场加载的情况,模拟结果比较的准确,快速获得结果,并且能够在非线性材料建模以及瞬态环境条件方面具有超强的功能,针对各种复杂的设计问题都能够很好的解决,帮助用户减轻压力,提高项目流程, 与依靠简化假设的线性FEA方法不同,Marc使您能够模拟现实行为和机械过程的复杂性质,以确保在现实环境和操作条件下具有最高的设计信心和产品性能。 自1971年以来,Marc被公认为世界上第一个商业非线性有限元分析软件,提供了创新,易于使用和强大的解决方案,非常适合分析经历几何,材料和/或边界的零件的结构完整性和性能。 非线性。支持模拟各种非线性的能力,即几何,材料和边界条件的非线性,包括接触。它也是唯一具有强大的制造仿真和产品测试仿真功能并能够预测损坏,故障和裂纹扩展的商业解决方案。结合其多物理场功能可帮助您耦合热,电,磁和结构分析,Marc是可满足您所有非线性仿真要求的完整解决方案。最新破解版下载,含许可证激活教程,欢迎有需要的朋友来本站下载体验!
功能特色
1、非线性和多物理场解决方案
针对非线性分析进行了优化的Marc提供了全面,强大的解决方案,以解决整个产品寿命中的问题,包括制造过程仿真,设计性能分析,服务负载性能和故障分析。这些包括:
包含所有形式的非线性(材料,几何,包括接触在内的边界条件)的非线性分析
热分析
耦合热力学分析
电磁学
压电分析
电热机械
静电和静磁以及结构响应
钣金成型,液压成型,挤压,吹塑,焊接,感应加热,淬火,固化,切割等制造工艺。
具有高阶3D元素的压电分析
2、接触分析
使用Marc出色且直观的联系人建模功能来研究多个组件之间的交互。
在1-D,2-D或3-D中轻松建立联系模型,分析和可视化不断变化的组件交互。
通过避免需要其他接触元件,接触对或从属主设备定义,提高建模效率。
无需额外的建模工作即可设置和研究自我接触。
轻松分析摩擦和相关材料变化的影响。
通过接近几何表面和热准则来控制接触行为
使用Marc中可用的自动联系人检测方法轻松添加,删除或修改联系人表定义。
搜索过程根据用户定义的或自动的接触公差开始。
3、非线性材料
从广泛的金属和非金属材料模型库中进行选择,以及用于结构,热,多物理场和流体分析的200多种元素的集合,以准确地对设计中使用的材料进行建模。
各向同性,正交各向异性和各向异性弹性
各向同性和各向异性可塑性
超弹性(弹性材料)
时间相关和时间独立行为
粉末金属,土壤,混凝土,形状记忆合金
焊料,粘塑性,蠕变
复合材料
压电
用户定义的材料模型
适用于高级材料模型(例如橡胶,塑料,热塑性塑料和金属)的广泛的材料数据拟合选项
物料数据可以存储到加密的物料数据文件中
4、失败与损坏
从一组全面的失效模型中进行选择,以研究金属,混凝土,复合材料和弹性体的降解和失效。
延性破坏
弹性体中的损伤累积
复合失效分析
层压胶合失败
低张力开裂和破碎
断裂力学
单调,低周期和高周期载荷下的裂纹扩展
用户定义的故障模型
使用Lemaitre模型的独立于网格的损伤预测
5、自动重新啮合
借助自动重新排列方案,以较少的建模工作即可获得更高的精度,从而确保在出现较大变形问题时确保较高的网格质量。
自动重新网格化2D和3D模型
用户指定的网格控制标准
有利于制造过程仿真和自接触分析
高阶3D元素可提高准确性
6、核心求解器技术
收敛Marc中久经验证的非线性技术使我们有信心为各种非线性问题开发可靠而准确的解决方案。
局部收敛控制以开发更好,更准确的解决方案。
同类最佳的收敛方法
MSC Marc 2020新功能
1、麦克斯韦蠕变模型的实验数据拟合
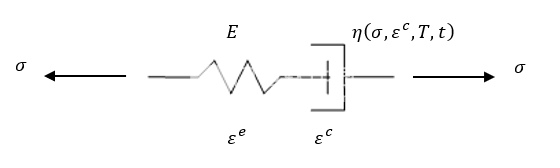
当负载持续较长时间时,许多材料会产生不断增加的不可逆应变。 这种蠕变现象存在于金属中,特别是在高温下,但也可能存在于塑料中。 Marc中描述这种随时间变化的行为的模型之一是麦克斯韦蠕变模型,该模型在流变学上可以看作是与非线性粘性阻尼器串联的线性弹性弹簧,如图1所示。
图1:蠕变的麦克斯韦模型
在此简要介绍数据拟合过程,以获取蠕变试验的实验数据,这些试验是在500小时的三种不同应力水平(150 MPa,175 MPa和200 MPa)下对钢合金样品进行的。 目标蠕变模型是时间硬化Norton-Bailey模型,给出为
其中ε̇c是单轴等效蠕变应变率,σ是单轴等效应力,t是时间,A,m和q是未知材料参数。
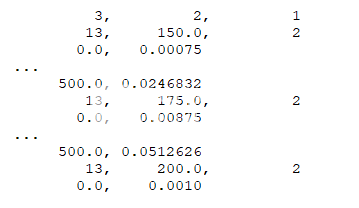
方框1:带有实测蠕变数据的衣衫table表
测试数据输入为方框1中所示的参差不齐的表格,其中包含每个蠕变测试随时间变化的测得总应变。 测量数据(输入)和拟合结果(输出)如图2所示。从拟合中找到的材料参数列于表1,相关的实验数据拟合菜单如图3所示。有关菜单的详细信息 ,支持的蠕变模型和参差不齐的表格,请参见“实验数据拟合”菜单的帮助菜单。
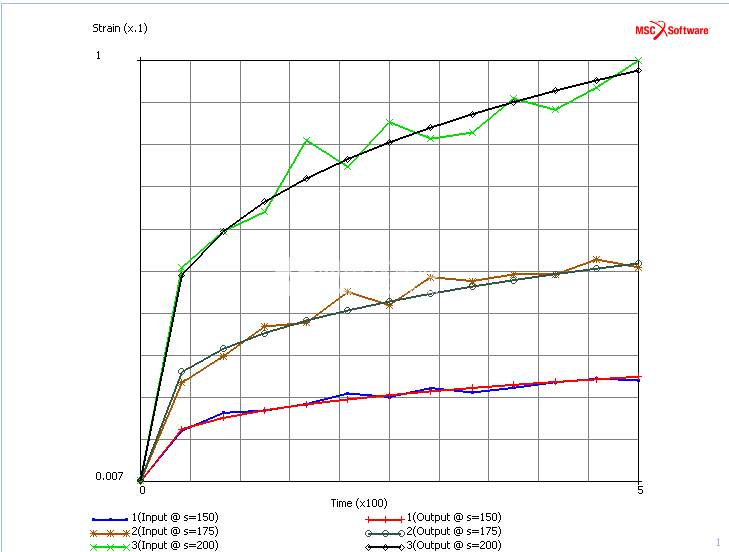
图2:测量数据(输入)与拟合(输出)
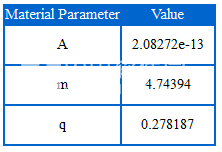
表1:时间硬化Norton-Bailey模型的材料参数
蠕变数据拟合过程包括以下步骤:
阅读表格和坐标表中包含实验数据的表格。 Syst。菜单并分配自变量。对于蠕变数据,第一个自变量是时间,第二个是等效应力。
在“材料属性”菜单中打开“实验数据拟合”菜单,然后从“属性”下拉菜单中选择“蠕变”(见图3)。
将表格分配给适当的测试。表格creep_test1被分配给应力深度。蠕变数据下的数据,如图3左上方菜单所示。
单击“蠕变拟合”按钮继续,这会弹出图4的“数据拟合材料模型”菜单。
通过选择幂律模型,将弹出图5所示的菜单,其中进行了特定设置:
在类型下激活蠕变测试;
选择所需的依赖关系(选择了“压力依赖关系”和“时间依赖关系”);
输入材料的杨氏模量,此处将其设置为200000.0 MPa
单击“计算”按钮开始拟合。一段时间后,图5下部菜单的Output部分显示已找到的材料常数,并且结果也以图形方式显示,如图2所示。可以在“ Data Fit Plot”菜单中进行更多的后处理(请参见图4)。 )。
单击“创建”按钮,可以在“材料属性”菜单中将估算的材料参数传输到新材料。
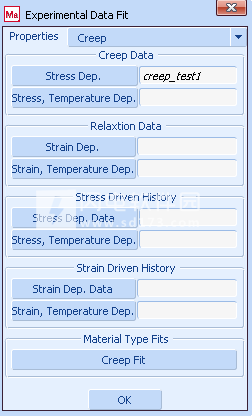
图3:实验数据拟合菜单
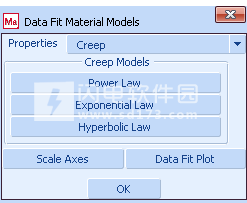
图4:“数据拟合材料模型”菜单
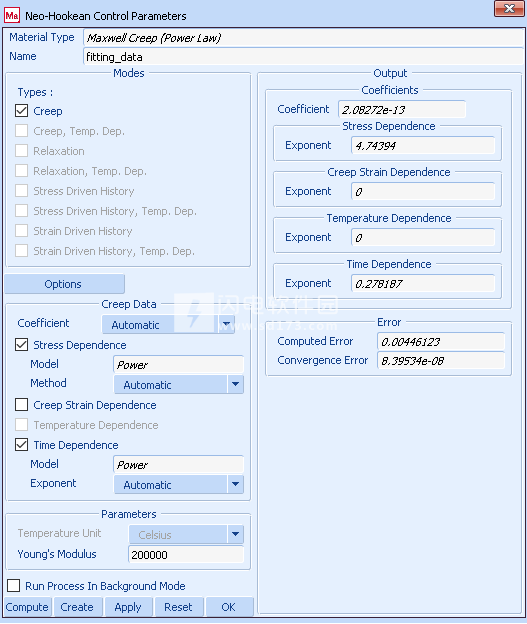
图5:用于拟合时间硬化Norton-Bailey模型的Maxwell Creep幂律参数菜单

2、Mentat中的分析维
使用Marc执行有限元分析时,用户可以选择完整的3D分析,但是在许多情况下,轴对称或平面模型足以分析当前的问题。
在以前的Mentat版本中,分析尺寸(3-D,轴对称或平面)的概念已作为菜单过滤器(在Element Types菜单中)被小规模使用,以隐藏菜单项。与所选分析维度无关。但是,所选的“分析维”未保存到Mentat模型文件中。因此,在打开先前创建的模型文件后访问此类菜单时,可能必须重新设置“分析维”。
从此版本开始,每个Mentat模型将具有定义明确的Analysis Dimension,将其保存到Mentat模型文件中,并在打开先前创建的模型文件时进行检索。分析尺寸可以是3-D,轴对称或平面。可以使用“分析工具栏”中的“分析维度”按钮(请参见图6)或通过“模型导航器”将其设置为创建模型的第一步。
图6:Analysis Dimension按钮
随着“模型分析维”的引入,所有菜单都得到了增强,从而在给定“分析维”的情况下,仅显示相关的模型选项和参数。 此外,已从“主菜单”和“模型导航器”访问的“新建”和“更改类型”下拉菜单中删除了“分析维”菜单级别。
当打开使用以前的Mentat版本创建的模型文件时,程序将从模型文件的内容中得出Analysis Dimension并进行相应的设置。 如果无法导出“分析维”,则将其设置为3-D。
从文件(例如Marc输入文件或Nastran BDF文件)导入数据时,分析维将从文件的内容派生。 如果无法导出“分析维”,则将其设置为3-D。
3、任意形状线圈的电流分布不均匀
使用Marc 2019,可以计算出横截面为任意但均一的闭合圆形线圈(即旋转体)中的非均匀电流分布。从2020年3月起,也可以在横截面为任意(且可能变化)的任意形状的开放式线圈(即具有起始和端面)中计算不均匀电流分布。这种新型线圈称为带端子的粗线线圈,可用于3-D和轴对称分析。
线圈的起点和端面称为终端面。每个终端面都有一个关联的节点,称为终端节点,可以在该节点上应用终端电流或终端电压边界条件。这允许人们在端面之间施加电势差,这导致电流流过线圈,或者规定通过线圈的电流,这导致端面之间的电势差。
终端节点可以由多个线圈共享。这允许一个人串联或并联连接线圈。例如,如果一个线圈的末端端子节点也用作另一个线圈的起始端子节点,则两个线圈串联连接:线圈中的电流将相同,并且两个线圈上的电势差等于各个线圈上的电势差之和。
在示例e020(第二种方法)中,演示了如何在轴对称分析中对六个带端子的空心线圈的串联连接进行建模。下面的图7显示了带有端子的单个3-D开路线圈的示例。在线圈的一个端子节点上,施加了交流电流。在另一个端子节点上,电压保持恒定。为了模拟快速流动的水,简化了水的温度,使其保持恒定。水和线圈之间的接触接触用于模拟线圈的冷却。线圈靠近铁板。流过线圈的交流电流会产生振荡磁场。后者在板内部产生感应电流,其结果是加热。
线圈和极板中计算出的温度和电流分布分别如图7和8所示。板中温度的细节高于线圈中的温度,如图9所示。很容易看出,线圈的形状反映在板中的温度分布中,并且温度在此处降低。线圈弯曲离开板。
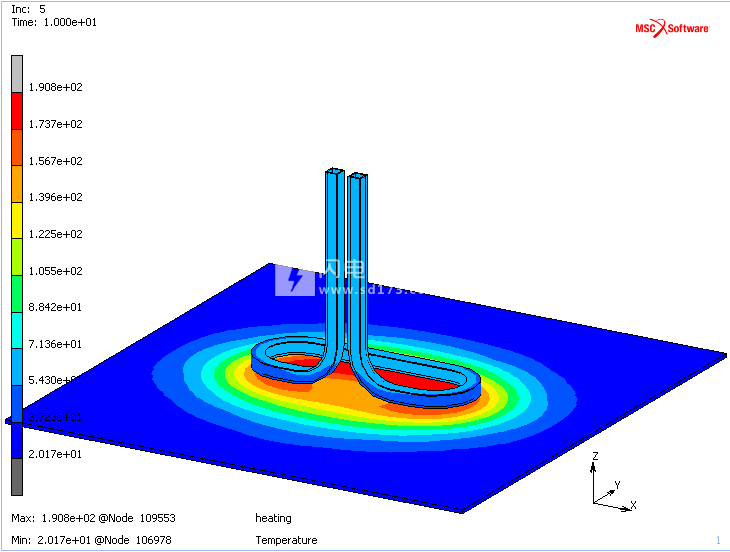
图7:线圈和板的温度
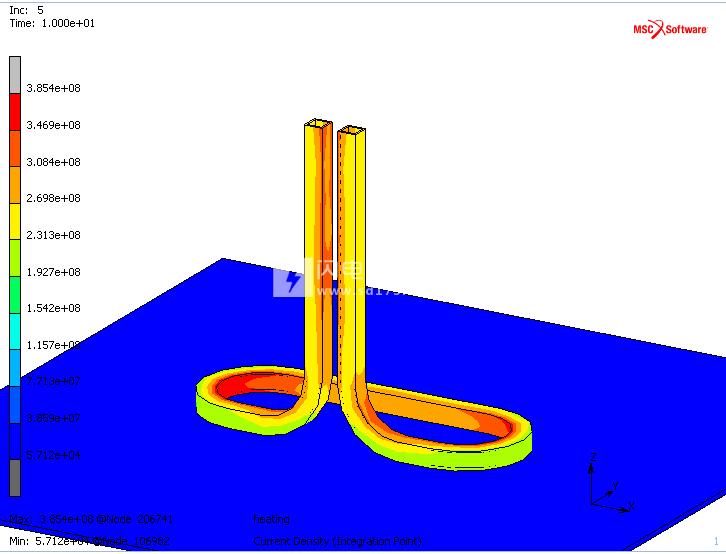
图8:线圈和极板中电流密度的等高线图
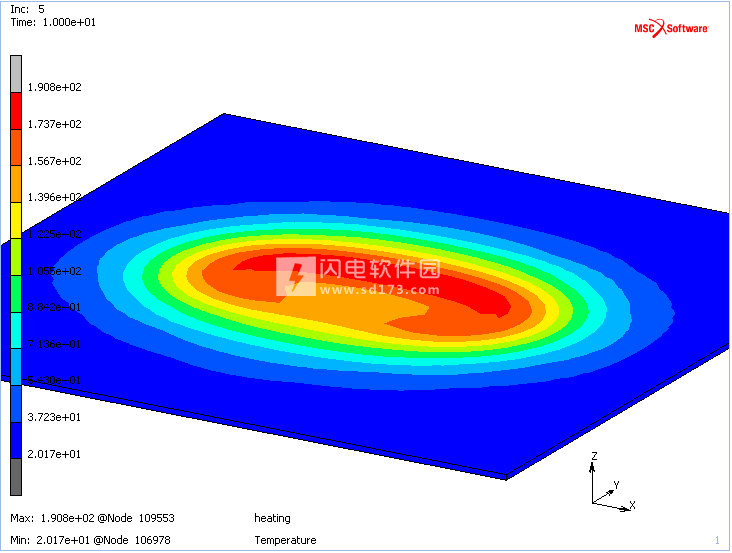
图9:板的温度曲线
4、段到段(S2S)接触的无应力节点投影
在段到段中,折线/多边形点用于表征触点对之间的接触面积。通过将法向偏移应用于关联的多边形点,可以实现触点对的无应力投影。该偏移量在每次Newton-Raphson迭代中连续应用,并且用户看不到。同样,对于有限滑动,当多边形点的相对位移超过滑动阈值时,将生成新的多边形点,并且没有将偏移量从旧点传递到新点的机制。应用偏移量的这种不连续性可能会导致收敛和精度问题。
最初的无节点应力投影已被引入以减轻这种情况。在分析开始时,对标记有无应力投影的任何物体对都执行节点投影。在该对的两个物体之间,在距离容差范围内具有更多接触节点的物体被投影到另一个物体上-即,将节点的坐标调整为放置在另一个物体上。进行一次节点调整后,仍然像以前一样在补丁的多边形点上计算并应用补丁级别的其他偏移。但是,由于节点投影,这些偏移量通常很小。
在分析图10中由两个接触体,一个圆销和一个支架定义的模型时,演示了已实现的无应力节点投影的使用。由于这两个物体的网格密度不同,因此位于销钉和支架之间的间隙和重叠部分可能导致结果产生虚假应力。
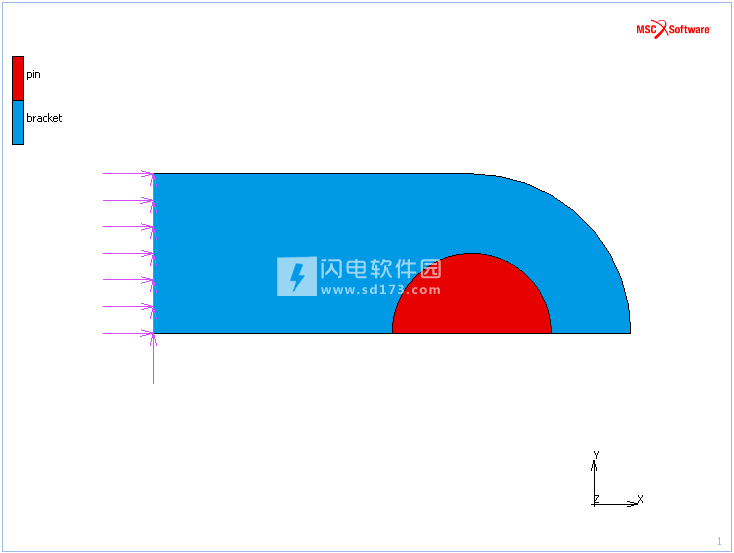
图10:用于演示S2S无应力节点投影的有限元模型
无应力算法首先计算节点投影。 由于销钉具有更细的网格,因此在分析开始时,其节点会投影到支架孔的表面。 默认情况下,所得的无节点应力投影将被写入后文件,如下图11所示。
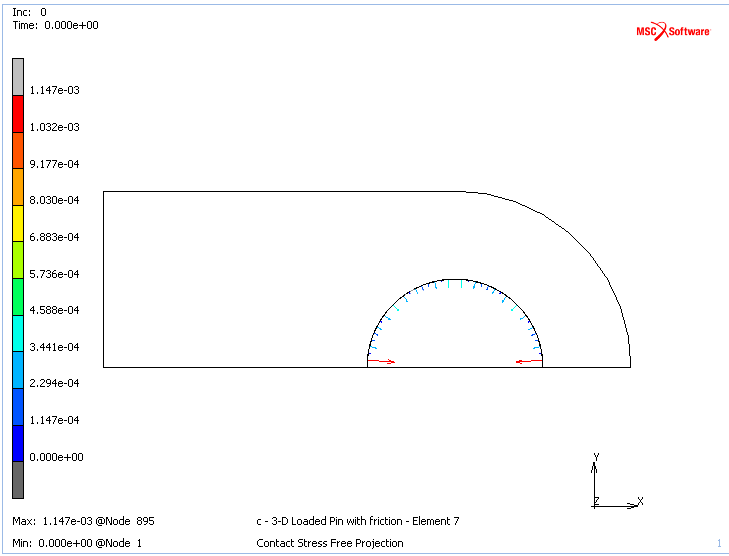
图11:两个接触体之间无接触应力的投影
5、节点到节点(N2S)触点的加速分离检查
引入了加速分离检查,以显着减少分离主导问题中的迭代次数,而不会影响分析的准确性。
在N2S接触中,默认情况下,仅在满足所有指定的收敛标准后才进行分离检查。如果用户指定了多个收敛准则,则在完成分离检查之前必须满足所有这些准则。例如,如果用户已标记“带有局部节点平衡和位移检查的残差检查”,则仅在残差在全局水平(模型中的最大残余力/模型中的最大反作用力<tol1)和收敛于水平时才检查节点分离。局部水平(节点上的最大残余力/节点上的最大单元力<tol2)和位移已收敛(模型中位移的迭代变化/模型中<tol3的位移增量变化)。如果分离检查表明一个或多个节点已分离,则将迭代计数重置为1,并继续进行Newton-Raphson过程。在许多分离主导的问题中,这种顺序检查会导致大量收敛性和分离性迭代。
引入了新的分离检查以解决此问题。一旦模型中的最大残余力下降到小于模型中最大反作用力的0.1,就检查节点是否分离。如果存在分离,则将迭代次数重置为1,并继续进行Newton-Raphson过程。如果没有分离,则继续迭代直到满足所有指定的收敛标准。
图12中的模型用于演示加速分离检查。在此工作中定义了四个载荷工况:前三个载荷工况用于分别对每个螺栓预应力,最后一个载荷工况用于在将螺栓锁定到位后加载锚固板组件。在所有工况下,都检查位移的收敛性,公差为0.1。
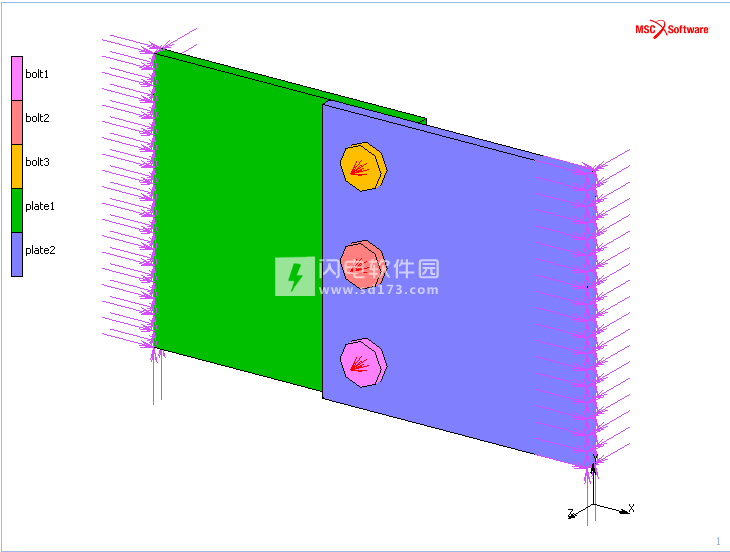
图12:用于演示加速分离检查的有限元模型
如图13所示,在Advanced Contact Control菜单中激活了加速方案,可通过以下按钮序列进行访问。

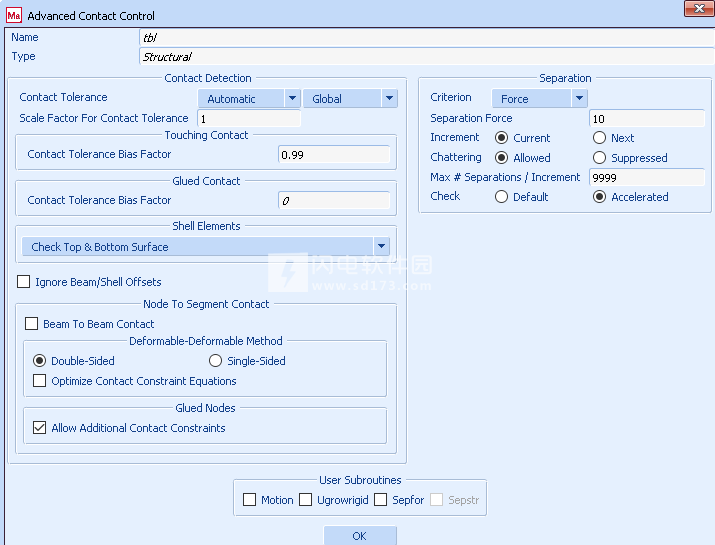
图13:高级联系人控制菜单
在默认方案中,仅在满足两个位移标准后才检查分离。 在加速方案中,在残差收敛到反应的0.1范围内或位移收敛(以较早者为准)之后,检查分离。 表2中提供了默认分离检查和加速分离检查的结果和运行统计数据的比较。使用加速分离检查可以显着减少迭代总数,而不会降低结果的准确性。

表2:N2S联系人分析的默认检查和加速检查之间的比较
6、线性接触
线性接触功能增强了线性和准线性模拟的接触能力。线性接触的主要考虑因素是位移和旋转非常小,并且零件开始接触。线性接触的典型使用场景包括发动机缸体分析和螺栓装配分析,接触体之间的相对运动有限。
使用“线性接触”选项,仅在分析开始时才建立接触,以后不会再有新的节点或线段接触。接触约束始终在初始配置中建立。接触实体可以在分析期间随时分离并重新建立联系。由于位移很小,并且零件最初处于接触状态,因此不会检查节点(节点到段)和多边形点(段到段)是否在段上滑动或穿透。由于忽略了接触约束中的非线性,因此此过程可导致较少数量的与接触相关的循环。
要选择线性接触,可通过以下按钮序列访问的图14中的“接触控制”菜单激活Mentat中的“接触类型”向下滚动选项:

图14:Contact Control菜单
图15所示的气缸盖接头模型用于演示线性接触功能。 分析中有四个荷载工况。 在第一和第二种工况下,左右螺栓依次受到预应力。 在第三和第四种工况下,气缸盖上的内部压力逐渐升高,然后释放。
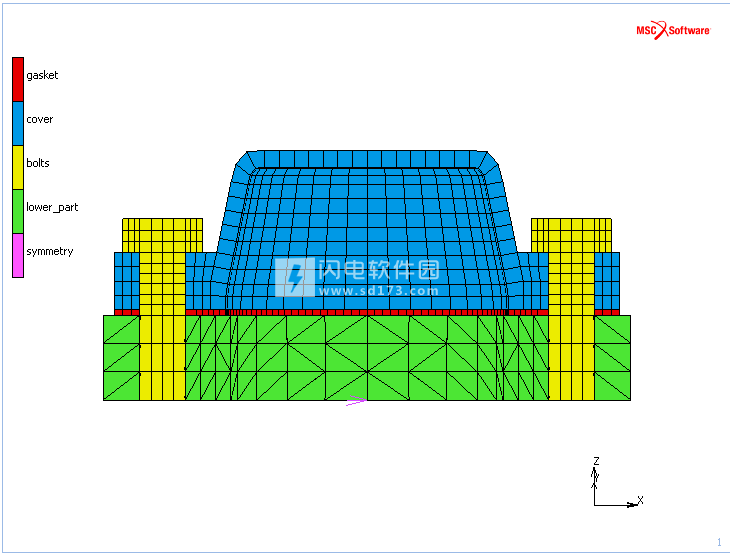
图15:气缸盖接头模型
表3显示,当使用线性接触而不是非线性接触时,迭代总数减少了,而对结果的准确性没有显着影响。

表3:非线性和线性接触类型的精度和性能比较
7、GPU对迭代求解器的支持
默认情况下,迭代稀疏求解器在CPU上处理。 在此版本中,迭代稀疏求解器已在GPU上实现,以缩短计算时间。 应注意以下几点:
GPU实施仅支持NVIDIA卡。
支持的GPU卡的最低计算能力为3.0。
支持的最高计算能力是7.0,这也是推荐水平。
建议使用专门用于计算的Tesla或Quadro卡,以获得良好的性能。
可以从命令行或从Mentat的Solver / Parallelization菜单中使用-gpu选项指定GPU卡的使用,如图14所示,可通过以下按钮序列进行访问:
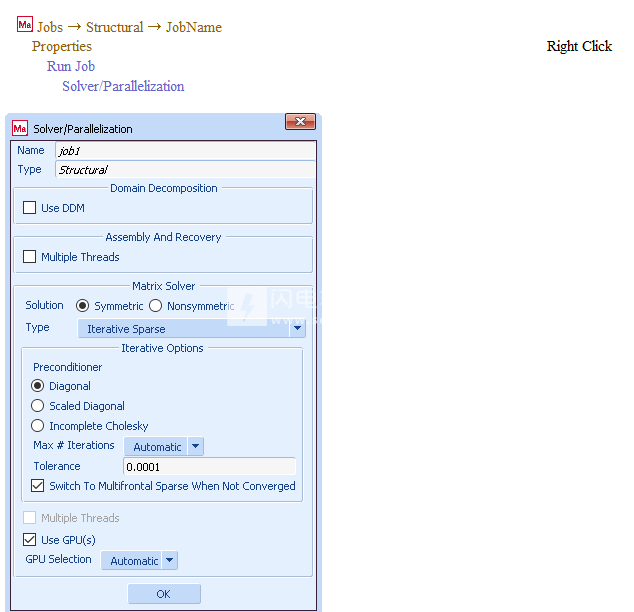
图14:求解器/并行化菜单
Marc安装的工具目录中的deviceinfo实用程序可用于确定可用GPU卡的ID。
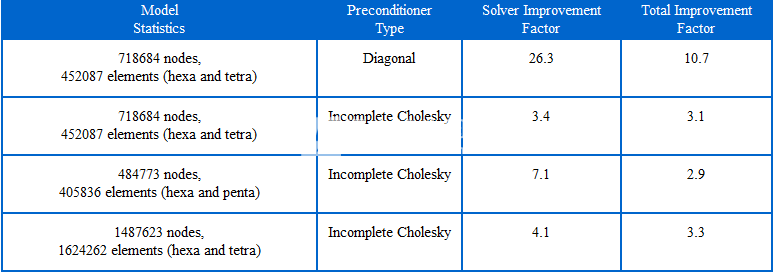
根据对多个大中型模型的基准测试(参见表4),发现GPU性能取决于模型大小,共轭梯度迭代次数,预调节器类型和已安装的图形卡。 允许的最大迭代次数是在运行时根据模型大小和预处理器类型自动确定的。 已经发现典型的性能改进因子对于对角预处理器为8到12,对于不完整的Cholesky预处理器为2到4。 用于获得这些基准测试结果的机器的详细信息如下:
操作系统:Red Hat Enterprise Linux Server 7.3版
CPU详细信息:
处理器:Xeon Gold 6126(Skylake)
记忆体:264GB
GPU详细信息:
卡:Quadro GV100
记忆体:32 GB
8、分析统计报告
从Mentat(作业属性➞运行)监视Marc分析时,将显示并不断更新Marc分析的各种特征(例如收敛率,增量数,分析时间等)。
在某些情况下,Marc分析可以成功完成,但是某些警告消息可能已打印在输出文件中。但是,除非打开输出文件以搜索警告消息的出现,否则用户不会知道它。
同样,在接触分析中,“迭代渗透性检查过程”(以避免接触体穿透)可能会导致迭代位移矢量发生缩放,因此可能会引入额外的Newton-Raphson迭代,而在监视分析时不会清晰可见。
在Marc Mentat 2020中,可以监视警告消息总数和已完成增量的分数。如果警告消息的数量不为零,建议检查输出文件中的警告消息(搜索字符串“ *** warning”),例如:可能指向用户做出的错误假设。如果完成的增量的分数从零缓慢增加到一,那么例如检查程序使用的接触公差的值(可能相对较小)或增量负载的大小(可能相对较大)。
9、Mentat易于使用
在Mentat中实现了以下增强功能:
在“结果文件导航”工具栏中,添加了“转到最接近指定时间的结果文件中的增量”按钮,以允许用户跳至最接近特定时间的增量。
已为用户介绍了以下常用的预定义表类型,以便可以通过以下按钮序列从Mentat主菜单中单击鼠标来创建它们:
Tables & Coord. Syst. ➞ Tables
➞ New
类型时间的预定义表
时间的线性斜坡
类型时间的线性上升和下降
线性斜坡到类型时间常数
将斜坡平滑到类型时间常数
时间步长
时间的三角形
类型时间的周期性步骤
类型标准化时间的预定义表
类型归一化时间的线性斜坡
类型归一化时间的线性上升和下降
线性斜坡到类型归一化时间常数
平滑上升到类型归一化时间常数
步骤类型标准化时间
类型归一化时间的三角形
类型归一化时间的周期性步骤
读者可以参考《用户指南》示例e003,该示例演示了时间Time线性斜坡类型的预定义表的用法。
在现有表中,用户可以删除两个选定或输入的点之间的数据点范围。
添加了一种简化的方法来提高实体的绘制精度,以增强实体的绘制效果。
可以在3-D空间中创建四面体。
复制实体时,新实体的名称与原始实体的名称绑定在一起(例如,如果用户复制了名为Steel的材料,则分配给新实体的名称为Steel(1))。
10、与Co-Sim 2020的兼容性
对于协同仿真分析,Marc 2020将与Co-Sim 2020兼容,并支持:
削减
行为的突然变化(例如由接触或可塑性引起)可能会导致Marc减少增量载荷,并重做增量(也称为削减)。 在2020版中,这将传达给Adams,并且将交换更新的数据(边界条件,力和刚度)。 没有与此功能相关联的新用户输入。
三通(Adams-Marc-scFLOW)
可以在作业属性➞分析选项➞协同仿真➞Marc-Adams-scFLOW中标记此过程。
使用液体进行流体(scFLOW)分析
对于几乎不可压缩的流体(液体),使用半隐式方法考虑了动压。 可以在作业属性➞分析选项➞共模拟➞Marc-scFLOW➞液体流量中标记此过程。 请注意,这不能与三通耦合程序结合使用。
11、弹性体的疲劳分析
在Marc 2020中引入了基于有限元的弹性体疲劳分析。基于有限元的材料特性以及所施加的载荷和约束,使用有限元分析来得出要研究的机械部件的应变场历史。 然后,将计算出的应变用于后续的疲劳分析中,以基于材料的耐久性来计算疲劳寿命和组件的损坏程度。
作为标准的疲劳材料模型,可以通过以下寿命曲线(有时也称为沃勒曲线)表达式来定义弹性体的疲劳特性:
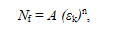
其中Nf是破坏的循环数,A和n是材料属性,而εk称为损坏参数。损伤参数可以是峰值最大主格林-拉格朗日应变或峰值最大对数应变,可以从疲劳分析之前的有限元分析获得。
除上述方程式外,还可以通过用户定义的表格输入材料的Wöhler曲线。
对于疲劳分析,可以使用各种加载条件,即恒定振幅加载,块加载序列和可变振幅加载。对于恒定的振幅负载,可以将上述方程式直接应用于确定故障循环数。对于块加载序列,采用Palmgren-Miner规则来计算疲劳损伤的累积水平。对于振幅可变的载荷,雨流循环计数算法用于将由有限元分析得出的变化应变的频谱减小为等效的应变振幅集。然后,通过类似于块加载顺序的Palmgren-Miner规则计算破坏程度。
用橡胶哑铃试样的有限元模型进行拉伸(有关更多详细信息,请参见Ayoub G.聚合物的大变形行为和疲劳:本构模型和疲劳寿命预测。博士学位论文,法国里尔大学1,2010)在Marc和Mentat中使用疲劳分析。如图15所示,已采用轴对称模型。
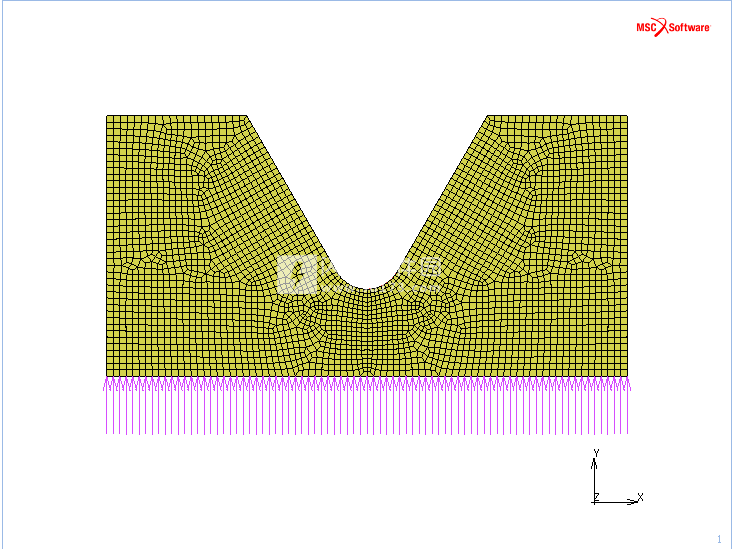
图15:橡胶哑铃试样的轴对称有限元模型
根据“幂律”模型在材料疲劳属性菜单中分配材料属性,并且采用最大主绿色拉格朗日应变作为损伤参数来定义Wöhler曲线(请参见图16)。 如图17所示,恒定的振幅载荷施加在橡胶部件上,并且结构分析的最后增量的结果用于疲劳计算。
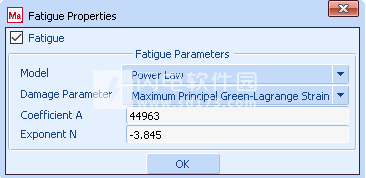
图16:材料疲劳特性菜单

图17:“作业疲劳属性”菜单
图18所示的疲劳分析结果表明,样品的失效将发生在中部,因为这导致失效循环的次数最少。 图19显示了故障循环数的对数等高线图,提供了有关故障分布的更深入的见解。 如预期的那样,样品的临界区域位于最小横截面的表面上。 同样的结论来自于损伤程度的等高线图,如图20所示。
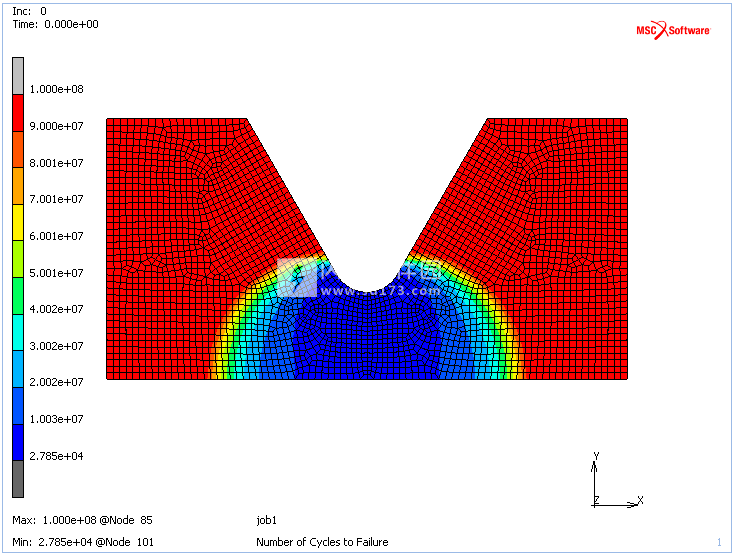
图18:故障循环数的轮廓图
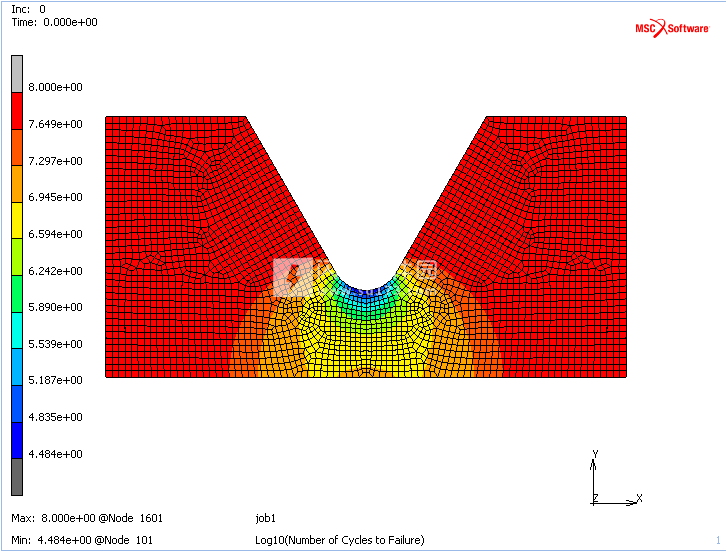
图19:失效循环数的对数轮廓图
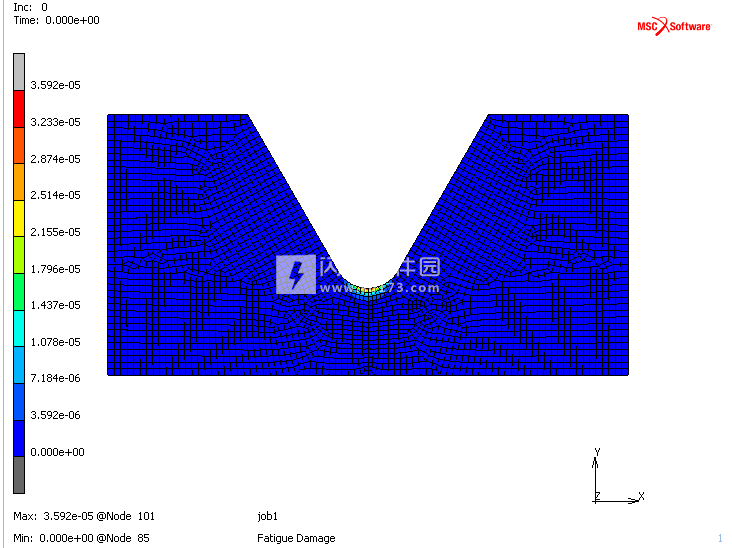
图20:疲劳损伤的轮廓图
安装激活教程
1、在本站下载并解压,装载m-mma20.iso,如图所示

2、首先我们来获取一个许可证,管理员身份运行破解文件夹中的MSC_Calc_20200715.exe,如图所示,输入Y,回车,然后自动在当前目录下生成license.dat许可证文件。先放着不管
3、安装MSC许可,双击破解文件夹msc_licensing_helium_windows64_a.exe进行安装,点击next,选择安装目录,如图所示,点击浏览选择刚才我们保存的许可证文件,许可证文件要放在安全的位置
4、许可证程序安装完成后,我们来安装主程序,双击marc 2020 windows64.exe运行安装,如图所示,选择软件安装路径
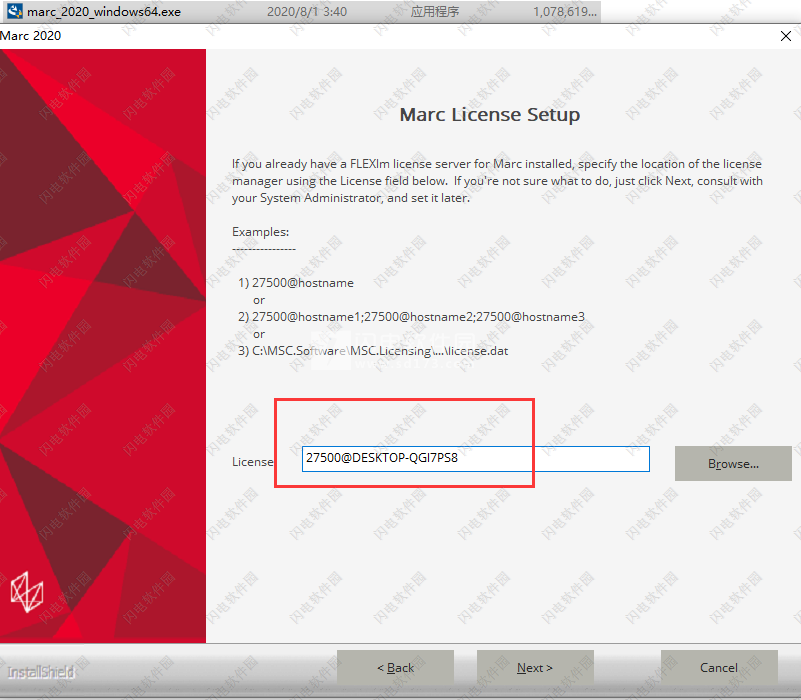
5、如图所示,这里填写27500@yourhostname,也就是27500@电脑名称
6、继续进行安装,安装完成,退出向导
7、最后如果有需要,也就是软件无法打开或者是报错,提示找不到许可证,这时候需要创建一个系统变量
变量名:MSC_LICENSE_FILE
变量值:License.dat的保存路径
闪电小编说明:
Marc 2020全新版本的智能非线性有限元分析程序,Marc是功能强大的通用隐式非线性有限元分析(FEA)软件程序,可针对各种设计和制造应用准确模拟静态,动态和耦合物理问题。新版本带来更多的功能,包括麦克斯韦蠕变模型的实验数据拟合、Mentat中的分析维、任意形状线圈的电流分布不均匀、段到段(S2S)接触的无应力节点投影、节点到节点(N2S)触点的加速分离检查、线性接触、GPU对迭代求解器的支持、分析统计报告、与Co-Sim 2020的兼容性、弹性体的疲劳分析、行业领先的非线性有限元分析求解器、最棘手的非线性问题的解决方案
 MSC Marc 2020 许可证授权激活教程
MSC Marc 2020 许可证授权激活教程
 MSC Marc 2020 许可证授权激活教程
MSC Marc 2020 许可证授权激活教程